假設有一個對x的定積分式

如下圖,如果f為折線的函式,則黃色區塊的面積即為自0到1積分的結果。
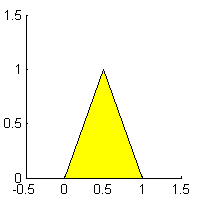
當然,我們很容易可以利用三角形面積公式,或者對f求定積分,而算出黃色區域的面積。然而,假設我們沒有這樣的先備知識,或者黃色區域的面積是難以求得的,那要怎麼辦呢?
跟據Monte Carlo method的想法,我們可以在包函定積分區域的一個範圍內,均勻取n個點。假設n=100, 且我們取的範圍是

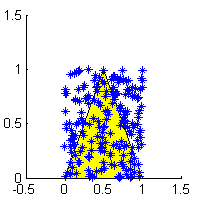
令[tex]n^*[/tex]為落在黃色區域內的點數,V為隨機取點的區域面積,而I為黃色區域面積,我們可以求得I的近似值。
[tex]I \approx \frac{n^*}{n}V[/tex]
這個應該很容易可以理解,我們在面積為1的區域中,隨機取了1000個點,若有502個點落在黃色區域中,我們可以估計黃色區域的面積近似於0.502。理論上n的數字越大,這個近似值會越準。但是上述的方法太慢了,利用高中數學就可以想到一個更快的方法 :)
令
[tex]g(x) = \left\{\begin{array}{ll}
1 & \textrm{,if x is in the domain of f(x)} \\
0 & \textrm{,else}
\end{array}
\right .[/tex]
則
[tex]I = \int_a^bg(x)f(x)dx = \frac{1}{v}\int_a^bg(x)f(x)Vdx[/tex]
令
[tex]h(x) = f(x)g(x)[/tex]
跟隨上面的推導,可以得到
[tex]I \approx \frac{1}{n} \sum_{i}^{n}h(x_i) = \frac{V}{n} \sum_{i}^{n}f(x_i)[/tex]
用一個很簡單的例子舉例,下圖 ((本圖取自英文維基百科此處))大家應該都覺得很眼熟,因為國高中的數學課本就出現過了。要估計一個函數所積分成的面積,我們可以在函數上取一些sample點,然後用sample點的高度和,乘上每個sample的平均寬度,就是這個區域面積的沽計值。事實上Monte Carlo integration就是基於這個想法。
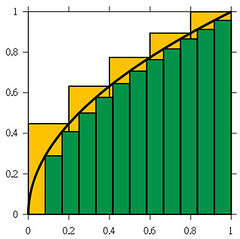
不僅止於此,這個方法還可以應用到較高維度的空間中。假設f的定議域由x,y...等多個變數所組成。則f的積分值可定義為:
[tex]I = \int_{x_l}^{x_u} \int_{y_l}^{y_u} f(x, y, \ldots) \, dx \, dy \ldots =\int_{V}f(x, y, \ldots) \, dx \, dy \ldots[/tex]
同樣的
[tex]I \approx V \cdot \langle f \rangle = \frac{V}{n} \sum_{i}^n f(x_i)[/tex]
只是此處V可能為取樣的體積(或超體積hypervolume)。這樣的方法比前一個方法可以少取樣一個維度,很明顯的可以加快演算法的運算速度。
Monte Carlo integration的方法是無法保證其誤差的error bound的,這一點可以很容易的觀查到。我們僅對空間做一些隨機取樣的動作,甚至不需要知道函數的細節,只要給與input能求的output就好了。因此,如果函數中有一個特別突出的區間,只要取樣點沒有落在那個區間上,就會造成很大的誤差。一般來說,要將誤差縮小n倍,則需要將sample點的數量乘上n平方倍。
在實作上,Monte Carlo integration還可以有不同的變化。例如在偵測到variance較大的區間,可以增加sample的密度以提高準確率等...
參考資料: